AI, Matlab, Unsupervised learning

K-means clustering algorithm from scratch

Matlab project.

K-means algorithm classes n observations into k clusters in which each observation belongs to the nearest cluster. 

GitHub link: https://github.com/Apiquet/KMEANS_algorithm

1- K-means explanation through an example

As it’s always easier to understand through an example, let’s see the following one:

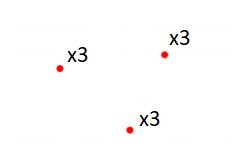
Imagine a 2D-dataset composed by 9 data points:

kmeanexample1

Then, applying a K-means algorithm with K equals to 3 would give the following result:

kmeanexample2

Each cluster took an average value of several data points. The following classification is performed:

kmeanexample3

Now, all the data points are relied to a cluster.

In the following part, we will compress an image with this method.

2 – Influence of K in image compression/reconstruction

2.1- Compression

To understand the influence of K, imagine that each data point (in the example above) represents a pixel in an image. An image of 3×3 pixels. Each pixel has a specific color. With a K-means process with K=3, we will create 3 new pixels that represents an average of several real pixels. Then we will save for each data point, which cluster is the closest. So, at the end of the K-means process we will only have 3 pixels in memory and a table with one number for each pixel that represents its closest cluster’s number.

2.2- Reconstruction

To reconstruct the image from that data, we will create 9 pixels (the number of row in the table) with the associated clusters. In our example, we will create 9 pixels with 3 different values (3 with the cluster 1, 3 with the cluster 2 and 3 with the cluster 3).

The result would be:

kmeanexample1
fleche
kmeanexample_reconstructed

2.3- Influence of K

We lose nuances in the process but the data is lighter in memory. However, the higher the K, the less nuances are lost! But the higher the K, the more memory the compressed image will take.

3- How to implement a K-means algorithm

3.1- Distance calculation

We first need to implement a function to get the distance between the data points. To achieve that we have several solutions:

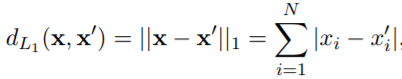
dist1
L1: Manhattan distance
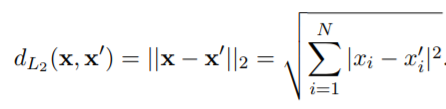
dist2
L2: Euclidean distance
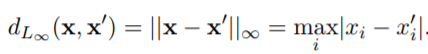
distInf
Linf: infinity norm
switch type
   case 'L1' % Manhattan Distance
      for i=1:N
         d=d+abs(x_1(i)-x_2(i));
      end

   case 'L2' % Euclidean Distance
      for i=1:N
         d=d+(abs(x_1(i)-x_2(i)))^2;
      end
      d=sqrt(d);

   case 'LInf' % Infinity Norm
      absDiff = abs( x_1 - x_2 ) ;
      d = max( absDiff ) ;
end

3.2-  Initializing K-means algorithm

To start implementing the K-means algorithm, we need to initialize a matrix Mu that has k columns that correspond to the k centroids. We can choose the k points randomly or uniformly:

if init == "random"
   for i=1:k
      index=randi([1 M]);
      Mu(:,i) = X(:,index);
   end
elseif init == "uniform"
   Mu(1,:) = datasample(X(1,:),k);
end

3.3- Implementing K-means algorithm

Our K-means algorithm will be composed of 3 main steps:

  • assigning each point to its closest cluster centroids:
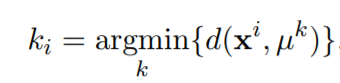
    eq_kmeans1
  • getting the label of the closest cluster:
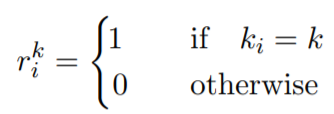
    eq_kmeans2
  • recomputing the centroids:
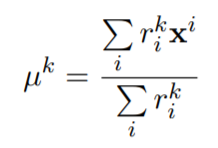
    eq_kmeans3
%Equation 1
[~,labels] = min(d_i);

%Equatin 2
for i=1:K
   for j=1:M
      if (i==labels(j))
         r_i(i,j)=1;
      else
         r_i(i,j)=0;
      end
   end
end

%Equation 3
for j=1:K
   Multiplication_Matrix = zeros(N, K);
   Sum = 0;
   for i=1:M
      Multiplication_Matrix(:,j)=Multiplication_Matrix(:,j)+r_i(j,i).* X(:,i);
   end
   Sum=Sum+sum(r_i(j,:));
   Mu(:,j)=Multiplication_Matrix(:,j)/Sum;
end

4- Result on real image

To see the real impact of K, we need to apply our algorithm on a real image. The following images show the result for K equal to 3, 5 and 11. The first one is the original image:

Kmeans_results
Visualization of the lost shades according to the K parameter

The code is available on my Github repository:

https://github.com/Apiquet/KMEANS_algorithm